Magnetic confinement fusion uses superconducting magnets to develop intense magnetic fields in which the particles that fuse are trapped. Performance is closely linked to the strength of the magnetic field. Doubling the magnetic field at the center of the plasma would, in principle, increase the fusion power released by that plasma by a factor of 16. The latest developments in high-temperature superconductors (HTS) pave the way for the use of even more intense fields, but at the cost of more intense electromechanical efforts. The design of these highly multi-scale and multi-physical magnetic systems is usually based on finite element models that are very costly in terms of computing power. CEA-IRFM has developed a reduced-order electromagnetic and mechanical calculation code to quickly assess the mechanical performance of these systems and carry out parametric studies. This work was presented at the 29th Magnet Technology International Conference in Boston, which brings together the entire superconducting community.
Facilities for the development of magnetic confinement fusion energy use superconducting electromagnets to generate high-intensity magnetic fields (10-13 T within the ITER magnets). SHTs offer an extended operating range and provide access to magnetic fields greater than 20 T. By exploiting these intensity levels, it is hoped that the size of plasma confinement chambers can be reduced while operating at the same fusion power levels, or that higher fusion power levels can be achieved. However, these magnets are subject to considerable electromagnetic stresses that increase with the square of the magnetic field. The mechanical strength of these components, in the context of compact high-field machines, therefore becomes critical.
As a general rule, volumetric finite element models can be used to evaluate the stresses induced in superconducting magnet structures. These multiphysics and multiscale models are very computationally intensive and require several hours of calculation for each configuration. The objective of the CIRCE (Cast3M Investigation and Research for Coils Mechanical Evaluation) code is to propose reduced-order models for evaluating the mechanical performance of a large number of configurations. This makes it possible to quickly identify critical points and structural limitations related to the increase in magnetic field.
CIRCE combines several modules (geometric, electromagnetic, and mechanical) and offers a complete calculation sequence for evaluating structural performance (Figure 1). The finite element models are based on 1D and 2D reduced-order formulations that greatly reduce the total number of calculation points and provide results in a matter of seconds. This approach has been validated [1] with models created for machines in operation or under construction, such as ITER and WEST. As the tool is parametric and flexible, studies on the Stellarator concept have been conducted in addition to the Tokamak configuration ([2] and Figure 2).
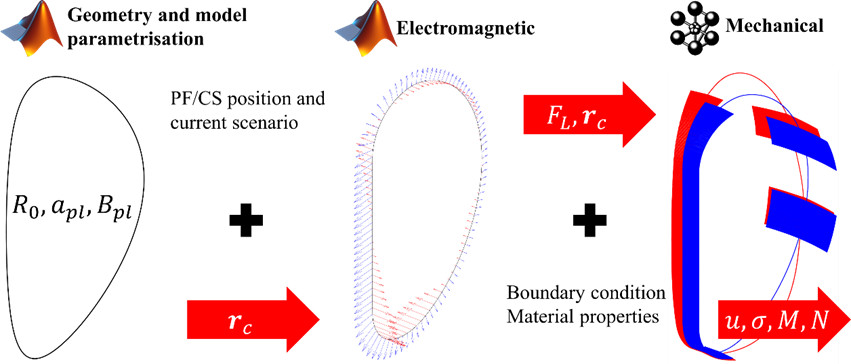
(input data, calculation of electromagnetic forces, then mechanical forces)
The CIRCE code focuses on the preliminary dimensioning of magnets for magnetic fusion devices and enables the rapid identification of limitations associated with increasing the magnetic field. It is part of the SF-Plant project of the SupraFusion PEPR, which aims to develop “system” codes describing all the components of a fusion power plant in order to assess the contribution of SHTs at a more global level and overcome the scientific and technological obstacles specific to these compact, high-field configurations.

on the HELIAS 5-B Stellarator
[1] B. Boudes, A. Torre, F. Nunio and C. N. T. Dao, “The CIRCE code: Cast3M Investigation and Research for Coils Mechanical Evaluation,” in IEEE Transactions on Applied Superconductivity, vol. 35, no. 5, pp. 1-6, Aug. 2025, doi: 10.1109/TASC.2025.3549395.
[2] B. Boudes, A. Torre, F. Nunio, R. Cubizolles, D. Biek and F. Lebon, “Update on CIRCE mechanical toolbox for fusion magnet system analysis,” in IEEE Transactions on Applied Superconductivity, pp. 1-5, 2025, doi: 10.1109/TASC.2025.3635641.


